В любом существующем бизнес-процессе реализована та или иная бизнес-технология. Мы хотим высказать свою точку зрения по двум вопросам:
а) инновационные бизнес-технологии;
б) оптимизация бизнес-процессов.
Инновационная бизнес-технология – это сочетание новых методов (способов) и современных инструментов (средств), которые при соблюдении определенных правил (стандартов, технических условий, протоколов) всегда приводят к гарантированному результату с точки зрения интересов конкретного бизнеса. Инновационная бизнес-технология отвечает на главный вопрос: «как вести конкретный бизнес так, чтобы его результаты были вне конкуренции в своей отрасли». Существующие бизнес-процессы в основной массе построены на устаревших бизнес-технологиях. Вышесказанное подчеркивает актуальность разработки инновационных бизнес-технологий для построения эффективного бизнес-процесса (рис. 1).

Рис. 1. Инновационная бизнес-технология и эффективный бизнес-процесс
Процедуры создания, последующего запуска и текущего обслуживания конкретного бизнеса также важны, но каждый бизнес, в конце концов, является отражением определенной бизнес-технологии. Аксиома: насколько инновационна выбранная бизнес-технология, настолько же ваш бизнес будет конкурентоспособным. Важный момент: каждая бизнес-технология является авторской, то есть разработкой конкретных людей.
Что такое оптимизация бизнес-процессов (бизнеса) и оптимизация в целом? В любом бизнес-процессе есть: а) поставщик – это тот, кто инициирует бизнес; б) потребитель – это тот, кто оценивает и принимает результат бизнеса. Бизнес – это последовательность конкретных действий, выполняемых с целью создания результата (ценности) для потребителя. Что касается оптимизации бизнес-процесса, то это процедуры, которые необходимо выполнить для того, чтобы рассматриваемый бизнес-процесс работал лучше.
Необходимо раскрыть суть термина оптимизация. В математическом смысле оптимизация – это поиск экстремума определенной функции (максимума или минимума) при заданных ограничениях. Т.е. при решении классической задачи оптимизации следует использовать некоторую математическую модель.
Перечислим компоненты стандартной математической модели задачи оптимизации: а) переменные (значения которых необходимо найти или вычислить); б) целевая функция – цель, записанная математически как функция переменных (необходимо найти ее максимум или минимум); в) ограничения (определенные из анализа конкретной ситуации и записанный математически).
Если оптимизация бизнес-процесса рассматривается как задача оптимизации в классическом смысле, то его математическая модель должна быть разработана заранее. Далее, основываясь на математической модели процесса и используя соответствующий метод решения, необходимо найти такую оптимальную (идеальную) схему процесса, чтобы конечные результаты (затраты, затраченное время, доход и т.д.) были оптимальными (минимальными или максимальными). Но функционирование бизнес-процесса не поддается формализации, из-за чего невозможно построить его математическую модель.
Мы делаем выводы. Невозможно оптимизировать бизнес-процесс в математическом смысле. На практике оптимизация бизнес-процессов относится к улучшению показателей эффективности бизнеса. Существует два типа улучшения бизнес-процессов: а) инжиниринг (незначительное улучшение); б) реинжиниринг (значительное, т.е. революционное улучшение) [1].
Чтобы оптимизировать бизнес-процесс, требуется четкое понимание того, чего мы хотим. Ситуацию можно резюмировать следующим образом: бизнес-процесс функционирует, но нас не все устраивает в существующем бизнесе. В приоритетном порядке анализируется текущая ситуация и формулируется цель оптимизации (например, увеличить выпуск продукции на 30% или снизить затраты на четверть).
Попробуем классифицировать существующие подходы к оптимизации (улучшению показателей) бизнес-технологий и бизнес-процессов.
- Методы (приемы), разработанные для рационального проектирования бизнес-архитектуры. Мы говорим о процедурах, которые выполняются как при внедрении нового бизнеса, так и при внесении изменений в существующий бизнес.
- Процедуры оптимизации, реализуемые при разработке новых бизнес-технологий.
Проектирование бизнес-архитектуры. Для описания архитектуры проектируемого бизнес-процесса, как правило, используется графический подход [2]. Графическое представление бизнес-процесса возможно в символах и по правилам специального «графического языка» – нотации. Вот основные характеристики наиболее распространенных нотаций IDEF0, BPMN, EPC (таблица 1).
Таблица 1 Основные характеристики нотации IDEF0, BPMN, EPC
| Сравнение | Нотации | ||
| IDEF0 | BPMN | EPC | |
| Что отображает? | Только структуру и функции бизнес-системы | Только поток процессов в бизнесе | Потоки событий и процессов в бизнесе |
| Чаще используется на уровне: | Верхний уровень бизнеса (над уровнем предприятия) | Для декомпозиции, для моделирования нижних уровней бизнеса (уровень предприятий) | |
Оптимальное проектирование архитектуры инновационного или действующего бизнес-процесса, осуществляемое с использованием графического подхода, является важной предпосылкой для обеспечения эффективного бизнеса.
Далее вопросы, связанные с разработкой бизнес-технологий в областях, где часть исходных данных в отношении проектируемых систем являются случайными величинами с определенными (или неустановленными) законами распределения. Например, бизнес-технология строительства торгового центра должна содержать рекомендации по нахождению рационального соотношения между количеством линий обслуживания клиентов и параметрами клиентского потока. Известно, что данные, которые являются основными параметрами клиентского потока, имеют вероятностный характер.
Рассмотрим методологию использования имитационного моделирования как одного из основных инструментов изучения сложных (вероятностных) систем.
Чтобы понять этот тип исследований, необходимо освоить основные понятия имитационного моделирования:
а) продолжительность одного прогона машинного эксперимента;
б) количество всех прогонов машинного эксперимента.
Источник [3, с. 61] содержит основные рекомендации по планированию машинных экспериментов:
а) короткие прогоны имитационных моделей с длительными наблюдениями в каждом отдельном прогоне более предпочтительны при планировании машинных экспериментов;
б) варианты с длительными прогонами имитационной модели с короткими наблюдениями в каждом отдельном прогоне менее предпочтительны.
В действительности, на стадии планирования машинных экспериментов не всегда соблюдаются основные рекомендации, изложенные выше. Например, в статье [4] продолжительность отдельного прогона (продолжительность периода моделирования) зафиксирована на уровне 15 месяцев без какого-либо обоснования. Это, конечно, чисто субъективный подход. Можно задать вопрос автору статьи: почему вы не выбрали 20 или 30 месяцев?
На самом деле, необходимо поэкспериментировать, сравнив результаты подходов «мало прогонов, но большая продолжительность одного прогона» и «много прогонов, но короткая продолжительность одного прогона». Какова цель? Необходимо достичь такого сочетания параметров имитационных экспериментов, при котором результаты моделирования достигают стационарных значений или наблюдается тенденция к стабилизации значений.
Неписаный закон метода моделирования: по мере увеличения продолжительности отдельного прогона должна наблюдаться сходимость значений результирующего показателя. Чтобы подтвердить вышесказанное, проиллюстрируем графически (рисунок 2) результаты задачи вычисления площади окружности методом имитационного моделирования, приведенные в источнике [5, с. 336].
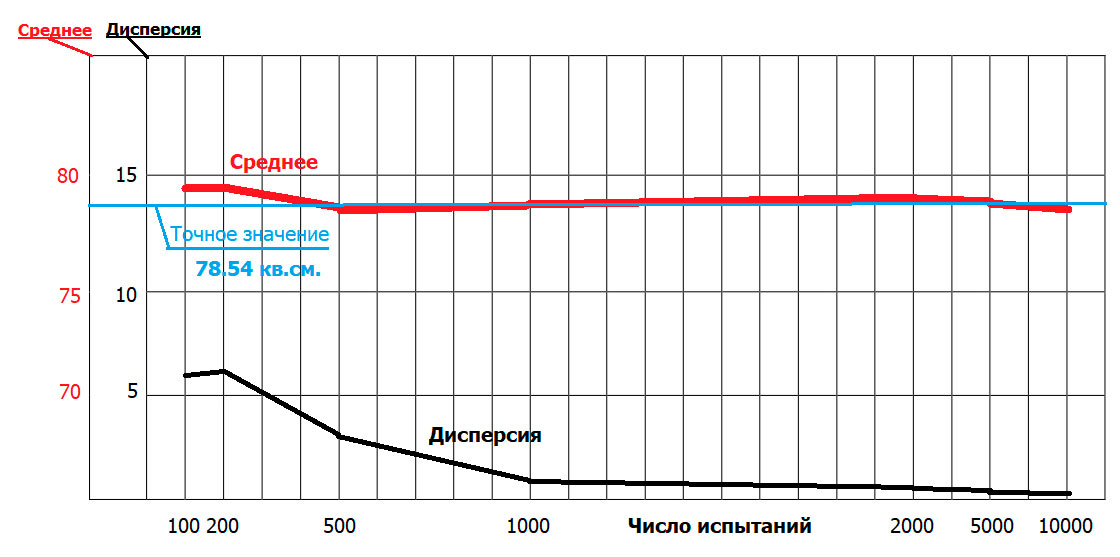
Рис. 2. Результаты изучения сходимости в задаче вычисления площади круга методом имитационного моделирования [5, стр.336].
С увеличением продолжительности одного прогона (количества испытаний) оценки площади круга приближаются к точному значению с уменьшением дисперсии, т.е. наблюдается сходимость (примечание: в примере каждый прогон рассматривается как отдельный эксперимент, состоящий из усредненных результатов десяти прогонов).
Мы изучили взаимосвязь между количеством прогонов и продолжительностью отдельных наблюдений в задаче проектирования системы управления запасами. Целью таких исследований является разработка методологии нахождения оптимального значения объема производства, которое минимизирует общие затраты (рассчитываемые в зависимости от наличия остатка или неудовлетворенного спроса).
Ниже приведен фрагмент исходного кода программного приложения (на C++), написанного и используемого нами для решения проблемы.
//—— ИСХОДНЫЕ ДАННЫЕ МОДЕЛИ
n = 5; // Начальный уровень запаса, шт
part = 40; // Объем производства в месяц, шт
mc = 40; sc = 5; // Спрос месячный: среднее и СКО (по нормальному закону), шт
ch = 60; cd = 60; // Стоимость хранения и Величина штрафа за не поставку, $ / шт
//—————————————————————
cout << endl << «Количество прогонов: «;
cin >> all_progon;
cout << «Количество месяцев в одном прогоне: «;
cin >> one_progon;
Исходные данные модели можно найти во фрагменте кода. В программе значения переменных «Количество запусков» (all_progon) и «Количество месяцев в одном запуске» (one_progon) вводятся с клавиатуры, что очень удобно для проведения имитационных экспериментов.
В таблице 2 приведены результаты имитационных экспериментов по схеме «мало прогонов, но большая продолжительность одного прогона».
Выяснилось, что при постановке имитационных экспериментов на моделях систем управления запасами отсутствует сходимость значения экономического критерия (общие затраты). Дело в том, что такие системы очень чувствительны к изменчивости значений входных данных.
Таблица 2. Средние суммарные затраты в $ (в процентах – коэффициент вариации)
| Прогонов: | Продолжительность одного прогона, количества месяцев: | ||||
| 100 | 200 | 300 | 400 | 500 | |
| 10 | 1677
66% |
1643
63% |
2609
46% |
2722
68% |
3018
57% |
| 20 | 1710
52% |
1916
54% |
3014
57% |
2474
49% |
2993
47% |
| 30 | 1532
60% |
2130
49% |
2170
47% |
3025
47% |
2860
49% |
| 40 | 1563
52% |
2369
60% |
2712
65% |
3290
58% |
3560
61% |
| 50 | 1403
51% |
2155
53% |
3034
58% |
2878
53% |
3307
65% |
Моделирование большего количества месяцев приводит к генерации набора максимальных значений спроса, что негативно скажется на выходных данных (в таких ситуациях общие затраты растут непропорционально). Следовательно, увеличение продолжительности отдельного прогона в системах обслуживания не приводит к стабилизации значений экономического критерия, а наоборот, наблюдается тенденция к его росту. Вывод: в таких задачах экономический критерий не может быть использован для обоснования параметров имитационного эксперимента.
Выводы. Инновационная бизнес-технология отвечает на главный вопрос современной экономики: «как вести конкретный бизнес так, чтобы его результаты были конкурентоспособными в своей отрасли». Если вы хотите совершить прорыв в своей отрасли, то внедряйте инновационные бизнес-технологии. Более того, вам не обязательно разрабатывать такую технологию самостоятельно. В настоящее время существует довольно много новых технологий, которые уже успешно внедрены в конкретный бизнес. Когда вы читаете об оптимизации бизнес-процессов, имейте в виду, что речь идет об улучшении показателей эффективности бизнеса. В области систем массового обслуживания экономические критерии не могут быть использованы для обоснования параметров имитационного эксперимента.
Автор
Нурышов Нурлан, магистрант
Атырауский университет нефти и газа имени Сафи Утебаева, (Казахстан, г. Атырау)
Библиографический список
- Майкл Хаммер, Джеймс Чампи. Реинжиниринг корпорации. Манифест революции в бизнесе»: Пер. с англ. – М.: Изд-во Манн, Иванов и Фербер, 2011. – 288 с.
- Каменнова М.С. Моделирование бизнеса. Методология ARIS. – М.: Весть-Мета Технология, 2002. – 333 c.
- Прицкер А. Введение в имитационное моделирование и язык СЛАМ II: Пер. с англ. – М.: Мир, 1987. – 646 с.
- Дагмирзаев О.А. Методическая помощь бизнес-аналитику в изучении особенностей решения оптимизационных задач при имитационном моделировании // Экономика и бизнес: теория и практика. – 2022. – № 9 (91). – С. 48-54.
- Таха Х. Введение в исследование операций: В 2-х книгах. Кн. 2. Пер. с англ. – М.: Мир, 1985. – 496 с.














